Update: Thanks as usual to Anschel for catching my typos!
This semester some grad students put together a learning seminar on the Poincaré homology sphere, where each week a different person would present another of the 8 faces from this classic (1979) Kirby-Scharlemann paper. It was a fantastic seminar that I recommend to any grad students interested in algebraic geometry, topology, geometric group theory, that sort of thing. I did the last description, which is actually description number 5 in the paper. You can read this post as a definition of the Poincaré homology sphere, without me telling you why mathematicians would care (but it has properties that makes mathematicians care, I promise).
First, start with a dodecahedron: this is one of the five Platonic solids, which are three-dimensional objects that can be created by gluing together regular (all sides are the same, all angles are the same) polygons so that the same number of polygons meet at any corner. The fast example of a Platonic solid is a cube (three squares meet at each corner), and a non-Platonic solid is a square pyramid (4 polygons meet at the top, but only three at each corner). If you glue two square pyramids together, you do get a Platonic solid, the octahedron.
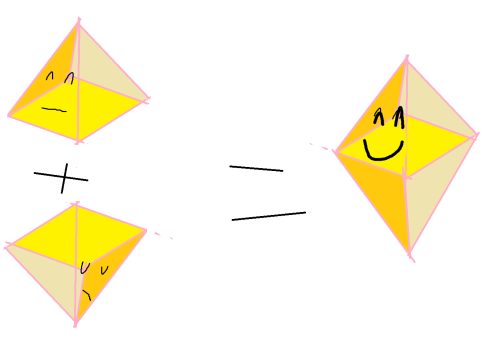
Glue two pyramids together along their squares sides, and now four triangular faces meet at each vertex and you have a Platonic solid: the octahedron.
So after all that build up, here’s a dodecahedron: 12 pentagons glued together the only way you can: start with one pentagon, glue five to it (one on each edge), glue those together into a little pentagonal cap with a toothy bottom. If you make two of these caps, you can glue them together; the teeth fit into each other just right. This is the first step in this AWESOME VIDEO below (seconds 30-45 or so):
To make a the Poincare dodecahedral space, let’s first review the torus. A long time ago, we learned about how to make a torus: take a square, identify opposite edges while preserving orientation.
First we glue the green arrow edges up together and get a cylinder, then the blue edge arrows together…
I’m a torus!
If you only identify one pair of edges and flip the orientation, you get a Mobius strip. If you do that to both pairs of edges, you get a Klein bottle, which you can’t actually make in three dimensions.
Mobius strip picture from wikipedia
This torus/Mobius/Klein side note is just to review that we know how to glue edges together. So look at the dodecahedron. Each pentagonal face has a pentagonal face exactly opposite it, but twisted by 1/10 of a turn (2pi/10). So if you identify each face with the opposite one, doing just the minimal turn possible, you get the Poincare homology sphere. We started with 12 faces in our dodecahedron, so this glued-up space will have 6 faces. It also has 5 vertices and 10 edges (vs. 20 vertices and 30 edges pre-gluing). I can’t draw it for you because it’s a 3-manifold. But here is a funny video of walking through it!
If you draw out all the identifications and you know some group theory, you can find the fundamental group of the thing, and you can prove to yourself that it is a 3-manifold and nothing funky happens at edges or vertices.
The dual to the dodecahedron is the icosohedron. “Dual” means you put a vertex into the middle of each face of the dodecahedron, and connect edges of the dual if the corresponding faces share an edge in the dodecahedron.
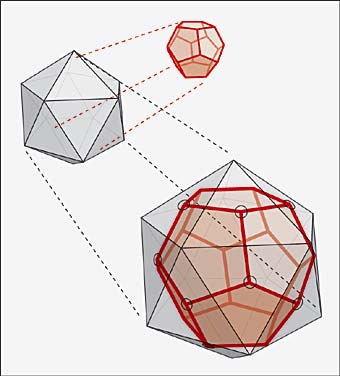
Image from plus.maths.org
So you can see that the dual to the cube is the octohedron , and the tetrahedron is its own dual. That’s all five Platonic solids!
Top row: tetrahedron, cube, octahedron. Bottom row: dodecahedron, icosohedron.
There’s more to the story than this! Let’s think about spheres. The 1-sphere is a circle in the plane, aka 2-space. Equivalently, the 1-sphere is all points that are equidistant from 0 in 2-space. Similarly, the 2-sphere is all points equidistant from 0 in 3-space. This gives you a notion of the 3-sphere. How can we picture the 3-sphere? We can use stereographic projection.
Here are the examples of stereographic projection of the circle and the 2-sphere onto the line and 2-space, respectively. You cut out a single point from the north pole of the sphere, and attach the space to the south pole as a tangent. Given some point on the sphere, run a line from the north pole through that point: it hits the space at exactly one point, and that’s the stereographic projection of the sphere-point. Notice that the closer you get to the north pole, the farther out your projection goes. If we pretend there’s one extra point (infinity) added to the plane, we can identify the n-sphere with n-space plus a point at infinity. Look at this link and buy things from it if you want!
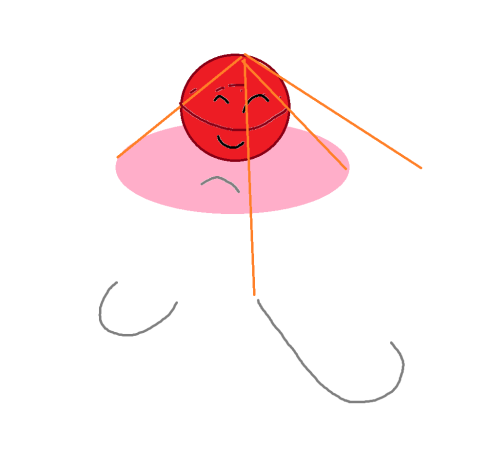
Projecting from the sphere to the plane: the bottom hemisphere of the red sphere maps to the pink circle in the plane, the top half maps to the rest of the plane.
What do circles that go through the north pole look like? Just like when we projected the circle to the line, they look like infinite lines.
So we can see the three sphere as 3-space, plus a point at infinity. Similarly here, circles that go through the north pole look like infinite lines.
Our math claim is that 
Start with one dodecahedron. Stack another on top of it, lining up the pentagons so you can glue one to another (that means the one on top is a 2pi/10 turn off from the bottom one). Now make a tower of ten dodecahedra, all glued on top of each other. Make a second tower of ten dodecahedra, and glue it to the first one (so it’ll twist around a bit). Glue the top and bottom of the first tower together (they’ll line up because we did a 2pi total turn); this’ll automatically glue the top and bottom of the second tower together. Nestle six towers like this together, so the toruses created from the towers all nestle together. Now you have a torus of 60 dodecahedra. Make a second torus of 60 dodecahedra. Put the second torus through the hole of the first, so you get a solid ball. (Here’s the weird 4-dimensional part!) That is a 3-ball! (The first torus also goes through the hole of the second one). So now we have tesselated the 3-ball with dodecahedra; this is called the 120-cell.
I might make a more technical second post on this topic explaining in detail the action, but suffice it to say that we have an action by a group that has 120 elements, so that if we quotient out this 120-cell by the action, we end up with just one dodecahedron with the faces identified the way we want them to (opposite faces identified by a twist). What is this group of 120 elements? It’s derived from the symmetries of the icosahedron, which has the same symmetries as the dodecahedron!
Final interesting notes on this: we identified opposite sides by just one turn. If you do two turns (so a 4pi/10 turn), you get the Seifert-Weber dodecahedral space. If you do three turns, you get real projective space.
More reading:
Jeff Weeks article on shape of space, a.k.a. is the universe a Poincare homology sphere?
Thurston book on geometry and topology
Fun website: Jeff Week’s geometry games
Baking and Math 
If you glue two square pyramids together you get an octahedron, not a tetrahedron. A tetrahedron, as the name suggests, has four faces, while an octahedron has eight.
There’s also a backslash missing for mathbb somewhere.