Tag Archives: doing math

Nytimes and algebra, again

9 Feb

Back in 2012, a professor named Andrew Hacker at Queens College in New York wrote an incendiary (to the math community) op-ed called “Is Algebra Necessary?”  I didn’t have a blog back then, but I did have a blog when a snarky and hilarious tweet appeared, and I posted about it/variables and algebra.  Tweet here:

This week, the NYT ran a short interview with Prof. Hacker, seemingly like a mild promo for his next book, “The Math Myth and Other STEM Delusions.”  A snarky and probably unfair summary of his previous books’ titles on sale at Amazon:  Blacks and Whites are separate and unequal in the US, Colleges suck, Politics from 1973, Women and Men are separate and unequal in the US, Rich and poor are separate and unequal in the US, Something maybe about gerrymandering?  My point is, this is an 86 year old man who likes to spin statistics about things people talk about the way Malcolm Gladwell likes to spin anecdata and make people talk about things, and he is also anti-math and pro-arithmetic.

Then I saw a video on facebook with over 4 million views of a woman explaining some “common core math” (see: old post on the wonderful thing that is common core standards) and how stupid she finds it.  But she surprisingly explains the steps carefully and it makes a lot of sense to me (though she skips why we add one of the 5s).  I actually love it: the kids can learn the concepts of why the answer is 30 rather than just a pure subtraction digit by digit shortcut algorithm that they can learn later.  Here’s the link; embedding isn’t working.

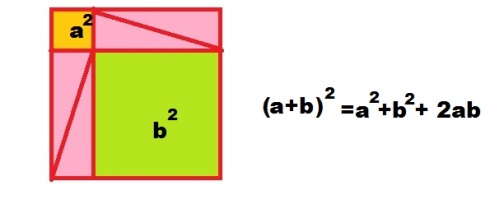
Throughout my time tutoring, teaching, and talking math, many, many students and adults have asked me “why do I need to know this?” and “how will this help me in the future?” and the conversations always seem to be two separate conversations.  “Math people” as we are sneeringly called by Hacker talk about something abstract [this is a link to an old but good blog post]: quantitative reasoning and logic skills, the ability to extract relevant information from paragraphs of data, visualization techniques, the ability to not be overwhelmed and taken in by misleading statistics and graphs.

Infamous unlabeled axes and generally “ethically wrong” graph from the Planned Parenthood hearing, from Americans United for Life website [quote from Politifact article]

Then there’s… not-math people?  Who want something more like this website which lists various jobs you use math in, and their median incomes.  Startling to me (I do not know where they get their numbers): they say biologists make medians of 44k, and mathematicians make 94k.  Anyways, mathematicians are used to abstract reasoning and use abstract terms as concrete ones (I can’t tell you how many times a week I say something like “Let’s use a concrete example like the plane” which is still a very abstract concept to many), which might explain the gap in this conversation.

I read an article this morning about the privatization of advanced math education and how rock and roll it is, but also extremely concerning in light of rising inequality.  Great article.  It gives me hope, especially this organization bringing advanced math to underserved communities.  I think that the ideal thing would be to have publicly funded school-year programs like UMTYMP available in as many places as possible, vs. having kids pay to attend summer camps like CTY, which offers some financial aid and also a gem of a paragraph on the financial aid FAQ site:

Families are also encouraged to seek funds from local agencies such as school districts, community service organizations, business associations, civic organizations and religious groups.

Note here that while I have TA’d at CTY summer camps before and had a blast, I never did them as a kid or even know about them.  I spent my summers playing as a middle school kid, and working or taking summer school as a high school kid.  (My high school summers: Health and Driver’s Ed classes, Boeing internship, working at Yoshinoya, working as a private tutor).  I really enjoyed them, but I think I also would’ve benefited from trying any of the various math/academic camps out there that neither I nor my parents knew about.  Then again, a bunch of my friends got sent to hagwon cram schools to memorize things and get great SAT scores during the summer, which sounds awful to me, so I counted myself as very privileged to be working a minimum or zero wage job instead.

I know the Common Core standards are young, but they’re also giving me hope that math is on the right track, and haters are gonna hate but kids are gonna learn and be able to do all those abstract things I said above.  I don’t have a lot to add to the conversation; this post was more to bring the Atlantic and NYTimes articles to your attention.

Tags: ,

Playtime with the hyperbolic plane

2 Feb

Update: Thanks to Anschel for noting that I messed up the statement of the last exercise.  It’s fixed now.  Thanks to Justin for noting that I messed up a square root.  Pythagorean theorem is hard, yo.

About a year and a half ago I explained what hyperbolic space is, specifically by contrasting it with Euclidean space and spherical space.  We’ve also run into hyperbolic groups a few times, which are groups whose Cayley graphs are somehow like hyperbolic space.  More precisely, a group is hyperbolic if, whenever you have a Cayley graph of that group, triangles are \delta-thin, which means the third side of any triangle is contained in a \delta neighborhood of the other two sides.  It’s important that the same \delta works for every triangle in the space.

thintriangles

Here the bottom side is contained in a neighborhood of the other two sides, and the triangle looks like it belongs in Star Trek

actuallythin

Here each side is contained in a small neighborhood of the other two sides, and it seems like the triangle is curving inward

Note that triangles in Euclidean space are way totally far from being \delta-hyperbolic.  For any big number n, you can make a triangle so that the third side is not contained in an n-neighborhood of the other two sides: just take a 2n horizontal segment and a 2n vertical segment to make an isoceles right triangle.  If n is bigger than 2, then the midpoint of the hypotenuse is farther than n away from the other two sides.  As usual, this long paragraph could be better done in a picture.

nothyper

Soooo not hyperbolic: you can make arbitrarily fat triangles in Euclidean space.  Also, the purple line should have \sqrt{2}}n as its length, not the square root of n.[/caption] I thought today we could just play around with hyperbolicity.  I'm running a small reading group on geometric group theory with some grad students, and today we got sidetracked a few times by just basic thoughts about geodesics in the hyperbolic plane.  We all thought they were interesting, so here I am trying to share it with you! There are lots of other definitions of hyperbolicity, but I like latex \delta-$thin triangles.  Oh I forgot to mention that a n–neighborhood of a point/line/shape consists of all the points within n of that point/line/shape.  So, for instance, a 3-neighborhood of a point in Euclidean space is a circle.  But with a taxicab metric, that 3-neighborhood is a squarey circle.

[caption id="attachment_3081" align="alignnone" width="181"]threeball Purple points are all distance three or less from red point

Anyways, I just put in that definition because it’s the first thing you’ll hear or see in a colloquium talk that involves the word “hyperbolic.”  Let’s play with the upper half plane model of hyperbolic space!  Here’s a repeat picture from that October 2014 post (wow that’s when baby was born!  He’s walking around and getting into trouble now, btw.).

hypspace

Straight lines are ones that go straight up to infinity, and segments of half-circles whose diameters lie on the bottom line

The graph paper lines in this picture are misleading; they contrast hyperbolic geodesics with Euclidean ones.  So the gray lines are Euclidean geodesics, and the colored ones are hyperbolic.  All geodesics in this model are either straight lines perpendicular to the horizontal axis, or semicircles perpendicular to the horizontal axis.  All of the horizontal axis and everything that the straight up and down geodesics end at (sort of like a horizontal axis infinitely far away) represent infinity.

I’ll write down the metric in case you were wondering, but we won’t need it for what we’ll be doing: ds^2=\frac{dx^2+dy^2}{y^2} [I took this formulation from wikipedia].  What this says is that the hyperbolic metric is a lot like the Euclidean one, except that the higher up you go on the y-axis, the less distance is covered (because of that 1/y factor).  More precisely, if you’re just looking at the straight line geodesics, the distance between two points at heights a<b is ln(\frac{b}{a}).

LINES

All the lines have the same length ln(2).  Blue: ln (8/4), green: ln (16/8)

The other fact we might want to know is that things that look like Euclidean dilations (stretching something like your pupil dilates from looking in a bright light to a dark room) are isometries in this model. You can see that in the picture above: the lines look like they’re stretching longer and longer in the Euclidean metric, but they’re actually all the same length.  Speaking of isometries, if you have any two geodesics (like a vertical line and a big old semi-circle somewhere else), you can find an isometry that sends one to the other.

First question: what do circles look like?  Whenever you have a metric space, it’s nice to know what neighborhoods look like, and the first thing you might want to consider are neighborhoods of points.  Turns out circles in this model look like circles in Euclidean space, but the centers aren’t where you think they are.  For instance, here’s a picture of circles with radius ln(2), which we saw in the straight lines above.

 

circles

The center of each circle is at the top of its surprised mouth.  The next highest line segment shows that each vertical diameter is actually a diameter (twice the radius).

Notice that the centers of these circles hang a lot lower in the circle than they do in the Euclidean metric!  Isn’t playtime fun?!

Generally when I play with math I throw out a lot of garbage ideas, and then eventually one of them is somewhat right.  Other people apparently think for awhile before they put out an idea.  Anyways, here are some sketches of what I thought a 2-neighborhood of a vertical line might look like:

NBHDS

This is the most subtle joke I have ever put in this blog

Maybe you looked at these and were like “Yen that is nonsense what were you thinking?!”  Maybe you are my advisor or a practiced mathematician.  Let’s go through the nonsense-ness of each of these pictures:

The rightmost picture is a 2-neighborhood of the vertical line in Euclidean space.  We know hyperbolic space is pretty drastically different from Euclidean space, so we wouldn’t expect the neighborhoods to be so similar.  The middle and left pictures have similar shapes but different curviness, and yes we’d expect a hyperbolic neighborhood to look different so those are guesses based in some more intution.  However, let’s try to figure out the actual size of a neighborhood of a vertical line.  We can use our previous pictures, and switch to a ln(2) neighborhood.

nbhdofline

Changed my mind this is the most subtle joke I’ve put in this blog please someone get it and appreciate it please please

Here I moved all our ln(2) circles so that their centers laid on the same line.  A neighborhood of a line is just the union of the neighborhoods of all of the points on that line, so if we just keep making ln(2) circles along the line we’ll end up with a neighborhood of the whole line.  So you can see that our actual neighborhood ended up being upside down from my middle picture above.  If this explanation didn’t make sense, here’s [half] a 2-neighborhood of a Euclidean line:

engb

Note how the denser the circles, the closer their boundaries on the left get to becoming that straight line we see on the right.

Actually using Euclidean intuitions and then mixing them up a bit is a great way to play with the hyperbolic plane.  This next exercise was an actual exercise in the book but it is just so crazy I have to share it with you.  It’s just dramatically different from Euclidean space, just like the triangles were.

If you have a circle in the hyperbolic plane and project it to a geodesic segment that it doesn’t intersect (which means for any point on the circle, you find the closest point to it on the geodesic and draw a dot on the geodesic there), the projection is shorter than ln(\frac{\sqrt{2}+1}{\sqrt{2}-1}).  Here’s the picture in Euclidean space where this makes no sense:

thirdplace

Third place likes getting on the podium.  I meant, the vertical lines show the projections from the faces to the horizontal line, and you can see they can be as big as you want if you just make bigger and bigger circles.

And here’s a picture in hyperbolic space that might make you think this could possibly just maybe be true.  Any circle will eventually fit inside a big huge circle that looks like the blue one in the picture, so its projection would be shorter than the projection of the blue one.  That means you only have to worry about big huge circles in that particular position.  And by “big huge,” I mean “of (Euclidean) radius n“.

exercise

Remember, if we’re just looking at vertical lines, we know how to measure distance: it’s ln(\frac{a}{b}).  So if you can show that the small orange circle hits the vertical line at \sqrt{2}n-n and the big orange circle hits it at \sqrt{2}n+n, you’ll have proved the contraction property.  Try using Euclidean geometry, and think about how we did the triangles case.

That was fun for me I hope it was fun for you!

Tags: ,

How to succeed in mathademia, by a grad student

26 Jan

This is, as far as I can tell, a great way to succeed in math academia.  But I’m only partway through the process and I’m not married to the idea of being in mathademia (I’m married to my spouse!).  Side story: some years back a professor was surprisingly denied tenure at a university where his wife’s family lived nearby.  He and his wife (and kids) then moved to a different country so he could be a tenured math professor there [it’s a good job].  I do not identify with this story.  I do identify with this: when I was a kid my mom would annually schlep us three kids to California from Minnesota for all two weeks of her allotted vacation time.

Outline of mathademia [I did not know all this til grad school]: you spend 4 years in undergrad somewhere that you want to go/live, then 5-6 years getting a Ph.D. somewhere you learn to enjoy going to/living (though no one cares how long you spend in grad school; I know one professor who took a six year break before going on), then 1-3 years doing a postdoc somewhere you often don’t want to live/go to, then possibly more of those postdocs until you get a tenure-track job somewhere that you better want to live.  After 6-7 years in your tenure track job, you either get tenure and will live there forever, or not and will have to go find somewhere else.  It’s all fairly civilized and organized.  Also, it gets more and more selective the further you go: I regularly hear about people applying to 80 jobs and getting 2-3 interviews and one offer.  Also, if you are romantically involved with someone else in academia, good luck with the two-body problem; almost every academic couple I know has had years of long-distance dating or marriage.

Undergraduate 

  1. Go to college.  While there (4 year liberal arts school or a university that offers PhDs both seem fine), major in math and take as many math courses as you can.  If possible, take graduate courses in math as an undergraduate.  If none are available, ask to take a reading course with a professor or a graduate student [for instance, several schools have grad-undergrad student reading programs like UT, UMD, UCHicago, Rutgers, UConn, Berkeley, MIT, Yale,  and more all the time].  For studying abroad, consider Budapest.  I did it and it was great!  I’m still in touch with friends from BSM and there are several in my field.
  2. While in college, do research.  Ask a professor for advice on doing a senior thesis project.  During your junior and/or sophomore summer, DO AN REU and get a little money to go to math research camp for a few weeks and hopefully get a peek into the publishing world.
  3. GO TO OFFICE HOURS.
  4. Also, study for the Math GRE during that same summer if not earlier.  Even if you’re a math hotshot it’s a hard test and you should study for it.  It’s only offered three times a year.  Note: some grad programs don’t require this.  Take the regular GRE too but there’s probably no need to study for it.
  5. Take the Putnam.  Do any extracurricular math activities you can.
  6. If you followed steps 1 and 2 you should be able to get some strong letters of recommendation for applying to grad school.  So, apply to grad school.  There’s lots of advice out there about this.  Also, while you’re applying to grad school, APPLY TO THE NSF GRFP and possibly NDSEG as well.  Note: this step is a lot of work!

Pre-graduate school

  1. Maybe you took some time between undergrad and grad school.  In that case, you’d better brush up on your math!  Some people have success in looking at their old notes/books/homework.  You could also check out these books: All the Math You Missed, Mathematician’s Survival Guide.
  2. If you’re a woman, consider doing this incredible summer brush up program that I did.  It’s great.
  3. Take 15 minutes and do this exercise.  First, quickly write down a list of five things that you value (for me: food, family, learning, math, creativity/writing).  Then choose one of the things and take five full minutes (time yourself) to write about why you value that thing.  Do so for two other things too.  I did this my first semester of graduate school with my roommate based on an article I can’t find anymore, but roughly was this one.  The point is that affirming your values and sense of identity can help you cope with graduate school.
  4. Figure out a physical exercise that you enjoy doing enough to actually do it.  If you’re already a gym rat or sports person, great.  If not, may I suggest Couch 2 5K.  Other things I’ve seen grad students do: rock climbing, cross country skiing, ballroom dancing, triathlons, marathons, swimming, yoga.  Physical activity really helps with the mental strain of first year of grad school.

Graduate school

  1. Swim in your own lane.  First and second year it’s easy to compare to other students who are in your same classes/have better or worse preparation than you.  After that it gets a lot harder and a lot more tempting to compare with your cohort.  Try to avoid this.
  2. Finish prelims/qualifying exams as quickly as possible, so you can focus on research = primary goal of graduate school.  This is how I studied for prelims: took the courses if applicable, downloaded all the previous exams (generally available on the department website), did one or two exams a week and checked answers with a study group once a week.  Study group = invaluable for problems that you aren’t sure how to solve.  Made a binder of all exams and all solutions (neatly written up) to reread at my leisure before exam.
  3. Talk to other graduate students, especially older ones.  Many programs have a big sib/little sib program for first years.  Exploit this.  Grad students know so many things that aren’t on the internet (which professors are good to TA for, shortcuts between classroom buildings, who wants what for exams or reading courses, what seminars to attend, who to ask for help).
  4. Publish if possible.  Find collaborators and publish results.  This is far easier said than done.
  5. Read read read.  Trawl arxiv every day (takes a few minutes) just to prime some words into your head/see who’s who in your field.  Read.  Reading math is HARD.  You need to do a lot of it in mathademia so you should try to learn how you do it best.  I take extensive notes while reading, others don’t.
  6. Give talks.  Every program has somewhere you can give a talk (1st/2nd year seminar, grad student colloquium, junior topic seminars) and you should give at least one before you start doing job talks.  It’s terrifying and then gets better the more you do.
  7. Go to seminars!  Every professor who has given me advice has said this to me.  I am not great about it but I think I have sleep apnea/mild narcolepsy.  My advisor is always falling asleep in talks too, which makes me feel better, but then he wakes up and asks intelligent questions which makes me feel worse.
  8. Take care of yourself.  Mental health days are legit.  Get physical exercise.  Eat well.  DO YOUR LAUNDRY, for all of our sakes.
  9. Go to at least one conference so people know you.  Follow your advisor around and have her introduce you to people in your field.  Try to give some talks at conferences.
  10. Applying to jobs is pretty much a full-time extremely stressful job.  So that fall semester of your last year of grad school, don’t expect to get a lot of math done.
  11. Write for the future version of yourself who doesn’t understand past you’s cryptic notation.  Write write write.  This is the ultimate goal of graduate school, to write a thesis.

Post doc

  1. Write write write.  Publish publish publish.  Collaborate.
  2. Make sure people care about your work, somehow (attend conferences, give talks???)
  3. ????

Tenure track job

  1. Write write write.  Publish publish publish.
  2. From my perspective, be superhumanly amazing and incredible.

Tenure

  1. Profit from your hard work!  Keep working hard because if you made it this far, you really love math and your work.  I’ve heard many professors say “why would I retire?” but I also know that teaching is draining.

ALTERNATE TRACK, STARTING IN GRAD SCHOOL

  1. Become a really good TA, and try to instruct your own courses.  Become conversant in things like flipped classrooms, IBL, clickers, and various pedagogy.  Consider doing math circle, DRP mentorship, tutoring.
  2. Write an incredible teaching statement, and personalize your cover letter to each teaching school you’re applying to.  Convince them that you love teaching.  Teach the letter reader something they didn’t know/think about before.  See notes I took from a talk by the president of the MAA:
  3. 20150630_150545.jpg
  4. Be an awesome teacher, and continue to do research on the side (depending on your position).

Note that I had a lot more advice for undergraduates than I did for after where I am now (I didn’t follow all that undergraduate advice either).  I also have no metrics really of “success” besides getting tenure, which is not for everyone.  I feel very successful life-wise with my family and blog and triathlons, but as to professional success I am pretty emo.  This blog post is about professional success==tenure.  Or you could be a badass and become a freelance mathematician or a mathematical writer  or anything else you want to be!  You’re getting a Ph.D. in math; the world is your oyster!

Also!  Writing this blog has been very fun and rewarding and one of the best parts is when undergraduates or beginning grad students or other people write to me to ask for advice or just say hey.  I love hearing from you!  I’m on email (yenergy), twitter (yenergy), and instagram (yenergyyy) so hit me up!

Tags: , ,

Best talk I’ve seen: Left orderable groups. Also, ask me about grad school!

30 Jul

This talk happened in March and I still remember it (and I was super sleep deprived at the time too).  Immediately after the talk, another grad student and I were chatting in the hallway and marveling at how good it was.  He said something like “I feel like a better person for having gone to that talk.”

A few days later, I ran into the speaker and told her that I had loved her talk, and she said “I’m super unintimidating so feel free to email me or ask me if you have any questions.”

During the talk, at one point she said (again, up to sleep-deprived memory coarseness)

“It’s more important that you learn something than that I get through my talk.  There’s no point in rushing through the material if you don’t take something away from this.”

All of these quotes are to say that this was probably the best talk I’ve seen (and I’ve seen lots of talks).  Particularly because of that last quote above.  Speaker put audience before ego, and that is a rare and beautiful thing (the other contender for best talk I’ve ever seen was by someone who recently won a big award for giving incredible talks).

Also, a quote from this fantastic and motivating handout which I wish I had had as an undergrad (or beginning grad student):

The good news is that this is something anyone can do – mathematics at this level is a matter of practice and good habits, and not “talent” or “genius”.

OK, done fangirling!  On to the math!

We’ll be talking about a property of groups, so brush up from a previous blog post or wikipedia.  First we need to define a  (total) ordering on a group: a binary relation ≤ that satisfies three properties (which you’d expect them to satisfy):

  1. Transitivity: if a≤b and b≤c, then a≤c
  2. Totality: for any a, b in the group, a≤b and/or b≤a
  3. Antisymmetry: if a≤b and b≤a, then a=b.

A few examples and nonexamples:

  • The usual ≤ (less than or equal to) on the real numbers is an ordering.  For the rest of this post, I’ll freely switch between using ≤ to denote being in the group, and being in the real numbers (it should be clear when we’re talking about real numbers).
  • Comparing heights of people is not an ordering: it’s not antisymmetric (see picture)
  • Ordering words in the dictionary is an ordering: if you’re both before/at the same place and after/at the same place as me, then we must be the same word.
  • Consider the group \mathbb{Z}_2\times\mathbb{Z}_2, which you can think of as a collection of ordered pairs $\latex \{ (0,0), (0,1), (1,0), (1,1)\}$.  If we define an ordering by (x,y)≤(a,b) if x+a≤y+b, then we’d break antisymmetry.  If we defined it by (x,y)≤(a,b) if x<a and y≤b, then we’d break totality (couldn’t compare (0,1) and (1,0)).
inequals

Top: reals are good to go. Middle: just because we’re the same height doesn’t mean we’re the same person! Bottom: (0,1) and (1,0) don’t know what to do

  • Can you come up with a relation that breaks transitivity but follows totality and antisymmetry?

Notational bit: we say that a<b if a≤b and a does not equal b.

Now we say a group is left orderable if it has a total order which is invariant under left multiplication: this means that a<b implies ga<gb for every g in the group.

Let’s go back to the reals.  If you use multiplication (like 3*2=6) as the group operation, then the usual ordering is not a left(-invariant) order: 2<3, but if you multiply both sides by -2 you get -4<-6, which isn’t true.  However, if you use addition (like 3+2=5) as the group operation, then you see that the reals are left orderable: 2<3 implies 2+x<3+x for every real x.  This is a good example of the fact that a group is a set and a binary operation.  It doesn’t make sense to say the real numbers are left orderable; you need to include what the group operation is.

Here’s an interesting example of a left orderable group: the group of (orientation-preserving) homeomorphisms on the real numbers. (Orientation preserving means that a<b means that f(a)<f(b), all in the reals sense).  If you don’t feel like clicking the link to prev. post, just think of functions.  To prove that the group is left orderable, we just have to come up with a left-invariant order.  Suppose you have two homeomorphisms g and f defined on the reals.  If g(0)<f(0), then say g<f.  If f(0)<g(0), then say f<g.  If g(0)=f(0), then don’t define your order yet.  If g(1)<f(1), then say g<f.  And so on, using 2, 3, 4…  Looks like a good left order, right?  WRONG!

Pink and blue agree on all the integer points, but not in between

Pink and blue agree on all the integer points, but not in between

If g and f agree on all the integers, they could still be different functions.  So we haven’t defined our order.  We need a better left order.  What can we do?  I know, let’s use a fact!

FACT: the rationals (numbers that can be written as fractions) are countable and dense (roughly, wherever you look in the reals, you’re either looking at a rational or there are a bunch in your peripheral vision).

So now we do the same thing, but using the rationals.  Enumerate them (remember, they’re countable) so use q_1,q_2,q_3\ldots in place of 1,2,3… above.  It’s another fact that if g and f agree on all rationals, then they’re equal to each other.  Let’s make sure we have an ordering:

  1. Transitivity: If f≤g and g≤h, then that means there’s some numbers (call them 2 and 3) so that f(2)<g(2) and g(3)<h(3).  But since we had to go to 3 to compare g and h, that means g(2)=h(2).  So f(2)<h(2), so f≤h.
  2. Totality: if I have two different homeomorphisms, then there has to be a rational somewhere where they don’t agree, by the second fact.
  3. Antisymmetry: We sidestepped this by defining < instead of ≤.  But it works.

Here’s a “classical” THEOREM: If G is a countable group, then it is left orderable if and only if it has an injective homomorphism to \text{Homeo}_+(\mathbb{R}).

Remember, injective means that each output matches to exactly one input.  Since we showed that there’s a left order on the group of orientation preserving homeomorphisms on the reals, we’ve already proven one direction: if you have an injection, then take your order on G from the order of the homeomorphisms that you inject onto.  So if h is your injection and g, k are your group elements, say that g<k if h(g)<h(k) in \text{Homeo}_+(\mathbb{R}).

One thing Mann does in her paper is come up with an example of an uncountable group that doesn’t do what the theorem says (she also does other stuff).  Pretty cool, huh?  Remarkably, the paper seems pretty self-contained.  If you can read this blog, you could probably do good work getting through that paper (with lots of time), which is more than I can say for most papers (which require lots of background knowledge).

That brings me to the “also”: I’ve been quite tickled to be asked about applying to grad school/what grad school entails a handful of times, some of those times by people who found me via this blog.  So please email me if you’re interested in whatever I have to say on the subject!  I’ve applied to grad school twice and have friends in many different departments and areas.  I hear I can be helpful.

Tags: , ,

Cool earrings and the Pythagorean Theorem

4 Jun

I’m so bad at suspense/surprises.  I wanted to write this post and say LOOK AT THE COOL THING AT THE END SURPRISE but instead I put the cool thing in the title.  In any case, last weekend I went to my college reunion and saw a dear friend who is doing an incredibly cool summer project about teaching and very thoughtfully teaches math to high school students during the school year.  She was wearing an amazing pair of earrings, which are the topic of this post.

https://instagram.com/p/3Ug9CvpM06/

Let’s look at them separately and then together.  First, the top, with the square embedded in the larger square.  We’re going to use some variables (which we talked about in this old post).  Notice that the triangles on the four sides are all identical right triangles.  Let’s label the sides of them: a for the short side, b for the longer leg, and c for the hypotenuse.

first

I LOVE visual proofs.  Personally I find them much more convincing than lists of equations with no pictures.  Spoiler alert that’s what we’re doing right now (visual proof, not a list of equations)!

Since the inner gray square is a square, and all of its sides are labeled by c, the area of the inner gray square must be c^2.

second

Once, during a calculus test, a student asked me for the formula for the area of a triangle.  I got mildly upset and said to think about it for a few minutes/come back to the question.  Eventually he got it, but I think it’s because another TA told him the formula.  Anyways, the area of the blue triangle is half of the base times the height, so it’s \frac{1}{2}ab.

With four blue triangles, we have a total of 2ab area from the triangles.  So the total area of the larger square is c^2+2ab.  But I can also look at the outside square.  Its sides are made up of one short blue leg and one long blue leg, so the large square side length is a+b, which means the outside square area is (a+b)^2.  Then the first earring gives me the equation c^2+2ab=(a+b)^2.

third

Now let’s look at the second earring.  I’m going to use the same variables since they’re the same triangles.

firstagain

Here, all four pink triangles are identical.  The orange square has a for all of its sides, and the green has b sides, so we know their areas.  We also still know the area of the pink triangles.

secondagain

If, like that calculus student, you happened to forget the formula for the area of a triangle, you can see it here: two triangles together form a rectangle with base a and height b, so the area of the rectangle is ab.  As the rectangle was made up of two identical triangles, you can see the area of each individual triangle is 1/2ab.

Again, the length of the side of the larger square is a+b, so the larger square’s area is (a+b)^2.

thirdagain

Summing up the orange square, green square, and four pink triangles gives another expression for the area of the larger square.

lastlast

So the earrings are both pretty cool separately- we got to prove that binomial expansion works in the second earring, and we got to play around with this technique with the first earring.  What if we put them together?  Both of the earrings have the same large area, which we decided was (a+b)^2.  So we can set the other sides of the equations equal to each other, and…

Party time!

Party time!

WHAT IT’S THE PYTHAGOREAN THEOREM WHERE DID THAT COME FROM THIS IS SO COOL!  Just look at how happy the squares are.  That’s how happy I felt when I saw Shira’s earrings, and also how happy I hope you feel after seeing them too.

Side note, I need to bake something.  Unfortunately those lime pies from a few months ago were so delicious that every time I feel like baking, I make those pies.  Another dear friend who does not do math asked me to try making pretzel salad, so that’s on the agenda, but my in-laws just visited and left a box of graham crackers.  Yes, we could feed them to the baby, but they’re just sugar and honey (which you shouldn’t feed to babies), so I’ll clearly make a graham cracker crust and might accidentally make another lime pie unless inspiration strikes.  We’ll see!

Tags:

The Apology and why it bugs me

3 Aug

I want to remark at the beginning of this post that I love math people.  We’re a little weird, very friendly, and generally quite open-minded and supportive (at least, this is true of the math people I know, a.k.a. geometric group theorists and friend fields).  There’s one thing that really, really bugs me that many (definitely not all) math people do when talking math with each other.

Also, I’m really into lists right now.

As I’ve mentioned earlier, I’m doing an exciting research program this summer involving four faculty, five graduate students, and three undergraduates doing at least five research projects.  With so many different experiences and different personalities interacting, there are lots of times when apologies are required:

  • Interrupting someone in the middle of a productive thought (actually people don’t apologize for this enough.  Reminds me of this post from the What is it like to be a woman in philosophy? blog)
  • Stealing someone’s notes/pen/paper/seat
  • Talking over someone (similar to the first thing here)
  • Probably more things I can’t think of right now

And I’m totally down with all of those.  They make complete sense- apologies are a nice lubricant for social and professional interactions.  But there’s one apology that really bothers me, which comes up in these situations:

  • Not knowing something that you’ve never been exposed to/had a reason to explore
  • Not being able to read the mind of someone who isn’t communicating clearly (related: this old post on teaching)
  • Having a different background than someone else, mathematical or otherwise
  • Being better at processing things in a visual rather than audial way, or vice-versa

These all come down to one thing: you’re a different mathematician than whoever you’re talking to.  And this is the thing that you might say in this situation:

Sorry, I’m slow.

I dislike this so much!  I’ve heard very many mathematicians say this over the past few weeks, whom no one would call “slow.”  One reason for my distaste ties in with the whole “women apologize more” bit, explored in a Pantene ad, dissected by Time, and perhaps most effectively explained in this spoken word video.

To be clear, this is not a women-only problem (while I’ve noticed more women do so than men, men also do this).  I dislike the phrase “sorry, I’m slow” because

  1. I’m apologizing for an adjective that I’m applying to myself- ->I’m apologizing for who I am.  [I am not a person who likes doing this.  I certainly apologize when I make mistakes/do bad actions, but to judge myself on my character, and invite you to pass that same judgment?  Not fun.]
  2. I’m devaluing my contributions to this conversation.  If I don’t take myself seriously, how can I expect you to?
  3. By saying these words aloud, whether I believe them now or not, I convince myself and you that I am, in fact, slow.  Just like if I looked in a mirror everyday and said “I’m ugly” I would eventually believe it.
  4. I’m perpetuating a system of these apologies- now whenever you’re in a conversation and struggling to understand what’s going on, you’ll be tempted to say “sorry, I’m slow” and cause 1-3 to happen to you.

Maybe the worst part of “sorry, I’m slow” is that there are good reasons to say it: when faculty/those further along say it, it encourages undergrads/younger folks that they aren’t the only ones who feel this way.  Similarly, if you say it in a group of peers, it builds camaraderie (in the way that teenage girls insult themselves in order to get compliments from each other).  When younger people say it to older people, mentorship instincts kick in and older people often share personal stories of some other time they felt slow.

Really what I’m saying is that “sorry I’m slow” is bad because it makes you believe that you’re slow, and it’s good because it tells everyone else that you also think you’re slow.  I just wish people didn’t pass these value judgments on themselves.  =(  I suppose this post is why I’m a mathematician, not a psychologist or sociologist.

From here: http://cheezburger.com/5218979584

From here: http://cheezburger.com/5218979584.  Also, I’m the puppy and the cat.

 

Tags: , ,

Two things I tell calculus students (one is the squeeze theorem)

22 Jun

I was subbing for a friend in our math tutoring center the other day and ended up chatting with an undergraduate who was retaking calculus.  She asked if I was a grad student in math, and when I affirmed, she said “wow, you must have memorized so many formulas.”  I laughed.  I told her that math is a lot like cooking.  Yes, you do need to memorize a few basics (how to cut an onion, general measurements like tsp to a TB, etc.), but you certainly don’t need to memorize every recipe you’re going to use.  You should definitely read them through and understand the rough idea of what’s going to happen; the more recipes you read, the better you’ll know how to use various ingredients.  And if you just pick up a cookbook and read a random recipe, maybe you’ll branch out to more exotic ingredients and figure out yourself how to incorporate rutabaga into your existing repertoire.

Hilarious photo from coursera (click for link)

Hilarious photo from coursera (click for link)

To make the analogy very clear: you should read and understand formulas, proofs, etc. very well, but no one expects you to be a walking textbook.  For a single class or a single exam, yes, you should know the info there.  But the idea is that from studying a theorem really hard for a while, you’ll remember the key idea for much longer than a semester.   Logic is hard, proofs are hard, math is hard.  You have to work really hard at the basics before you can make a perfect souffle.

Another way this analogy works: no one learns to cook by memorizing cookbooks.  You learn to cook by getting your hands dirty in the kitchen, trying out random recipes from the internet, and burning a few more complicated things that you weren’t ready for.  If you’ve never chopped vegetables with your dad in the kitchen as a kid, sure, you start at a disadvantage, but that doesn’t mean you can’t pick up a knife and try.  Use youtube videos, ask friends, cook with friends!  Now replace all the times I said “cook” in this paragraph with “math” and pretend that math is a verb.

Check out this cookbook! There are similar math books

Check out this cookbook! There are similar math books

Students (like me) often think we won’t cut it in grad school because we don’t have the experiences of others- didn’t do undergraduate research, take graduate courses while in undergraduate, maybe didn’t even major in math.  But just because you didn’t help your parent as a kid doesn’t mean you can’t cook now, and just because you didn’t focus on math before doesn’t mean you can’t do it now.  You learn to do math by doing math.

So that’s the first thing I tell calculus students, or at least this one that I was talking to last week.

Second thing: she asked me to explain the squeeze theorem to her.  Will do!  My explanation of it involves an old family curse.

So when my little brother was born, someone who was mad at my parents cursed our family.  Luckily they weren’t too mad, so it was a pretty benign curse: I would always be shorter than or the same height as my oldest brother, and I would always be taller than or the same height as my baby brother.  (Another way to say this: I’ll never be taller than my big brother, and my little brother will never be taller than me.  This affects our sibling basketball games, but that’s about as bad as the curse gets).

I think this is pretty good considering I googled 'basketball' and 'basketball hoop'

I think this is pretty good considering I googled ‘basketball’ and ‘basketball hoop’

We grow up, and we always grow according to the curse.  One day when we’re grown ups, someone sees my two brothers and realizes that they’re the same height.  Without even seeing me, they can answer: How tall am I?

… (this is you thinking)…

Yup, I’m the same height as those two!  This is the squeeze theorem, because my brothers’ heights has squeezed mine.

Replace our heights with functions: let’s say my brother’s names are Gerard and Hugo, and indicate their heights at time x by g(x) and h(x), respectively.  And I’m f(x).  Since Hugo is always taller than or the same height as me, we have an inequality: $latex f(x) \leq h(x)$ for all time x.  Similarly, $latex g(x) \leq f(x)$.  Putting these two together, we have g(x) \leq f(x) \leq h(x). 

The squeeze theorem says that if for some a where all three functions have a limit, \displaystyle \lim_{x\to a} g(x) = \lim_{x\to a} h(x) = L, then we have forced ourselves into \lim_{x\to a} f(x) = L, just as Gerard and Hugo’s heights forced mine to be the same as theirs.

Two things I tell calculus students!  I actually tell calculus students a lot of things (like calculus not using family curses), but these are the two things I told a calculus student last week.

Tags:

On not giving up

3 Dec

On my very first day of high school, my calculus teacher had me take a pre-test to make sure I belonged in the class.  I was the first freshman of that ridiculously excellent school’s history to be in calculus, which was entirely due to the INCREDIBLE program at the University of Minnesota, UMTYMP– if anyone you care about is a 10-12 year old in the greater Twin Cities area, I highly highly suggest checking out the program.  The next night my parents were extremely concerned about me, as I was in tears over my calculus homework.  I thought that I wasn’t good enough and that it was too hard for me, rather than that perhaps I was less prepared or mathematically mature than expected (see my post on whether we should do math at all for more thoughts in this direction).  I still ended up rocking both years of AP calculus, and doing okay at Cal State Fullerton, where I took a few more math courses during my remaining years of high school.

I made this picture all by myself

I made this picture all by myself

It’s been over a decade since my first math tears, and about three years since my last ones- I struggled so much over integrals over contours in my complex analysis course, and definitely had tears spring to my eyes when I finally lugged myself over to the math tutor (incidentally, I had some beer with him over the summer at a conference and he is awesome) to ask about one particular problem.  I was ridiculously heartened when he didn’t immediately spit out an answer, and told me that “the most important thing is to stay calm,” which kept me from nervous breakdowning at a total stranger.  When handing back exams to my calculus students, I’ve definitely noticed a few hastily wiped tears and debated on commenting and potentially embarrassing them, or letting it go and feeling like a callous ass for the rest of the day.  Now I tell them the story in the next paragraph.

A few months ago, after doing that mini-triathlon, I saw a groupon for Crossfit and thought I’d try out what I affectionately call the “cult.”  I’ve mentioned before that I’m incredibly weak, and I’ve definitely noticed this during my crossfit classes- I’m an okay runner, but in terms of strength I’m last, and definitely lag behind the pregnant woman (who is a beast).  Until yesterday I’ve been completely at peace with this, because I can tell I’m getting stronger and improving and feeling pretty good, even when the trainers have to set up separate stations for me because I can’t do a push up with good form.  At my last session we had a coach I hadn’t met before who started us all with the same strength, and gave us a few minutes to fiddle with it and add more weight as needed.  It is clear to me now that the burden was on me to speak up or simply do my thing and give myself less weight after trying out the initial condition, but I was too shy/ashamed to help myself do my best, and I ended up sabotaging myself and finishing my workout with many, many tears because I felt inadequate and incompetent.  I’m glad that I finished, but the coach had to lessen my weight partway through and I did one less round than the other women.

The moral is that we aren’t all born with the same strengths.  As my boyfriend said when comforting me that night, some of these women in this class have been playing sports since middle school, when I was doing Destination Imagination and Future Problem Solvers, or at least did athletics in high school, when I was playing clarinet in the marching band.  And that’s OK.  Those women will be lifting more than me, and I will be doing the best I can with what I have.  Not everyone in my calculus section is going to be an A student- they never learned algebra and are working two jobs to support themselves through college, so don’t have the time to master algebra and pass their other actual classes.  That’s OK.  What’s important is that they finish the workout and give it the best they have.  And tears are OK too, they happen to all of us.

Tags: ,

Brainstorming, also, Cantor sets

10 Jun

So I studied for those prelims for a few months (maybe two) on my own, reading old notes, highlighting things, rewriting relevant proofs, running through my homeworks, attempting extra exercises from the textbooks, the usual extreme studying.  I don’t know about you, but I am SO MUCH BETTER with other people when doing just about anything.  Knowing someone else will eat my baked goods makes my baked goods better.  Being accountable to a colleague makes me justify my ideas more and I write down fewer false things.

Math is a creative endeavor.  People seem to think mathematicians are somewhere between human calculator, engineer, and crazy person.  But we don’t get grouped with, say, artist, writer, poet, all that often.  I’m going to quote some wikipedia here:

Plato did not believe in art as a form of creation. Asked in The Republic,[18] “Will we say, of a painter, that he makes something?”, he answers, “Certainly not, he merely imitates.”[16]

Now, as with many creative things, there are certain tools you can use to help with math.  Going on walks is a good thing.  Eating breakfast.  Naps, even.  But the thing I love, and the thing that helped me pass my prelims (whoooo), is brainstorming.  A few weeks ago I read an article that a facebook friend posted (isn’t it funny how you know what I’m talking about when I say “facebook friend” rather than “friend”?  In this case, a guy I went to high school with) about how brainstorming is basically stupid and broken.  And, given the parameters that the article offers, it’s pretty right: get in a group, generate lots of ideas, don’t be critical.  I don’t have a lot to say about brainstorming (though Jonah Lehrer for the new yorker and a guy from Stanford’s d.school do and these are both fascinating), but I do have things to say about problem solving with a group.

Brainstorming, as this three-step outline is, isn’t the way solving problems with a group should be done.  He’s on point with steps one and two, but step three should be different: be critical.  Fight for your ideas.  Fight other people’s wrong ideas.  I work with other grad students a lot, and I often don’t realize that I’m completely wrong until I’ve been talking about an idea for a few minutes.  I need them to fight me in order to learn and understand and be better.

The idea behind brainstorming is that if you’re critical of others’ ideas, they won’t want to share them and will clam up.  I absolutely felt that way for the first year or so of graduate school- I would feel that my peers shot me (personally) down, and that I didn’t have any good ideas.  What finally changed my mind and made me more combative was realizing that I do have good ideas, sometimes.  Not all the time, probably not even 50% of the time, but sometimes I’m right, I’m absolutely right and I can prove it if you-just don’t shoot me down or interrupt me or dismiss me.  These last three things still happen, and I’ve learned to fight back in a nonconfrontational manner- it’s easier in my case because everyone in the room just wants to reach a solution.  Some people have egos (I do too), but we learn to listen to each other to the extent we’re capable, and to make each other listen when we can’t extend ourselves to do so.

Basically, I agree with this guy: “Innovation Is About Arguing” is the first bit of his title.

On a totally different topic, let’s talk about the Cantor set.  It’s a pretty cool subset of numbers with lots of unintuitive properties.  Building it is fairly straightforward.  Look at a number line.  Focus only on the segment between 0 and 1.  Cut the segment into thirds, so you’ll have notches at 1/3 and 2/3.  Delete the middle third (1/3,2/3) so you end up with two segments.  Do this over and over again, deleting the middle third from each segment you have at any one point.  Look at the picture

 

I DID NOT MAKE THIS PICTURE it is from wikipedia.

And you just do that forever.  A few cool things about this set:

  • It contains no open intervals, since we’d cut out the middle third from any interval that showed up.
  • Despite that, no points in the Cantor set are isolated: if you take a point in it and look in a teensy neighborhood (like, \pm .00000001 teensy), you’ll still find other points from the Cantor set.
  • It’s uncountable, which means literally that you can’t count it , even if you had infinite time.  Counting numbers are countable (1,2,3…), and so are numbers that can be written as fractions (1, 2, 1/2, 3/4…), but all the numbers between 0 and 1 aren’t (this is Cantor’s diagonalization argument, which I’ll blog about some time).  You can show that the Cantor set is uncountable by making a function from it to the interval [0,1], which hits all the numbers between 0 and 1.  If it hit all the numbers between 0 and 1, we say the map is surjective or onto [0,1].  If it’s surjective, then for every number in [0,1], there’s a number in the Cantor set that maps to it, so the Cantor set is bigger than or equal to [0,1] in size.  Since [0,1] is uncountable, this means Cantor set is too.
  • If you consider the set C+C = \{x+y : x,y\in C \}, you get an interval, which is way incredible and unexpected because it contains no intervals- it’s like putting together two sets of discrete bread crumbs and magically having a loaf.

You think about that last bullet point, and I’ll do a post later proving it.  Hint: know how we can think of any number as a decimal expansion?  Well, you can also use base 3 and do a ternary expansion, so 1/3 = 0.1, 2/3 = 0.2, 4/9 = 1/3+1/9 = 0.11, etc.  The Cantor set, by the way we defined it, is all the numbers between 0 and 1 that contain no “2”s in their ternary expansion.

Hasta later!

Tags: , , ,